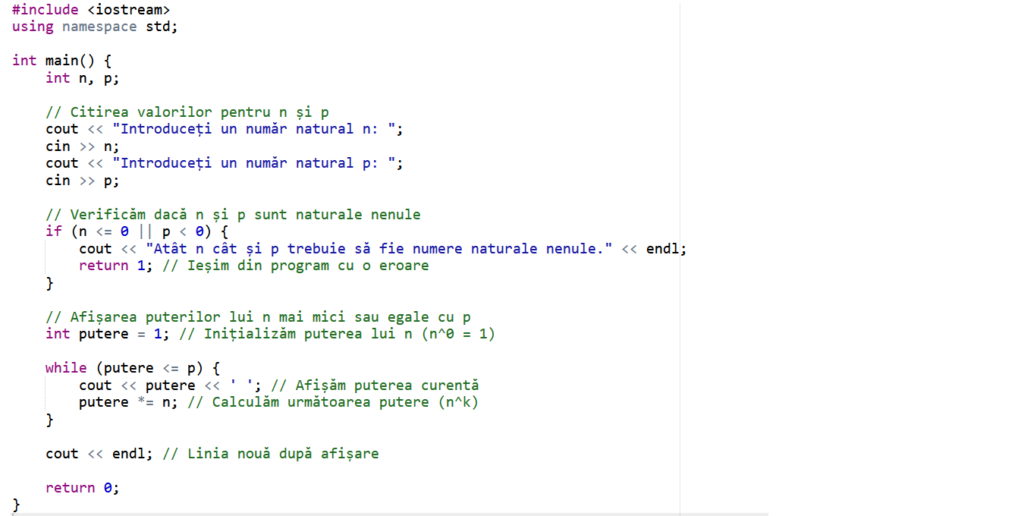
1.Se dau două numere naturale nenule n și p. Afișați în ordine crescătoare puterile lui n mai mici sau egale cu p.

Ex.Date de intrare 3,100 Date de ieșire 1 3 9 27 81

2.Se citesc numere de la tastatură până la apariția lui zero. Să se determine câte dintre ele erau pare.

Ex.Intrare 1 2 3 4 5 6 0 Ieșire 3

3.Să se afișeze suma cifrelor unui numar natural n de cel mult 9 cifre.

4.Să se afișeze produsul cifrelor impare ale unui număr natural n, de cel mult 9 cifre. Dacă numărul nu conține nicio cifră impară, se va afișa -1.

5.Se citesc două numere naturale, n – un număr natural de cel mult 9 cifre și c – o cifră din mulțimea {0,1,2,… 9}. Afișați de câte ori apare c în scrierea numărului n.

6.Se citește un număr natural n cu cel mult 9 cifre. Afișați oglinditul lui n.
Exemplu: pentru n=1234 se va afișa 4321.

7.Se citește un număr natural n cu cel mult 9 cifre. Afișați mesajul este palindrom sau nueste palindrom dacă numărul are sau nu această proprietate. Un număr este palindrom dacă este egal cu oglinditul său.
Exemplu: pentru n=1234321 se va afișa este palindrom.

8.Se citește un număr natural n cu cel mult 9 cifre. Afișați cifra maximă și cifra minimă.

9.Determinarea si afisarea cmmdc(cel mai maire divizor comun) pentru doua numere citite de la tastatura folosind algoritmul lui Euclid

10.Dându-se un număr natural n, să se afle suma primelor n numere naturale (1 + 2 + 3 + … + n).

11.Dându-se un număr natural n, să se calculeze suma cifrelor sale, după aceea suma cifrelor a sumei cifrelor sale, și așa mai departe până când se ajunge la o singură cifră. Să se afișeze această cifră (deseori numită cifra de control a numărului).

12. Să se afişeze pentru un număr întreg x cu cel puţin 3 cifre şi cel mult 9 cifre:

a. cifra unităţilor

b. cifra zecilor

c. prima cifră din stânga

d. numărul format din primele două cifre din dreapta

e. numărul format din primele două cifre din stânga

f. numărul format din prima, a treia, (a cincia) etc. cifră din dreapta